The Wodarz lab conducts interdisciplinary research by designing mechanistic computational models of biomedical processes, both predictive and explanatory. Collaborative interactions with experimental and clinical laboratories are central. The goal of collaborating across disciplines is the emergence of new insights that would otherwise not be possible. The work falls into three broad areas: (i) Computational models of carcinogenesis, cancer evolution, and cancer therapy; (ii) Computational model of the in vivo dynamics between viral infections and immune responses; (iii) Evolutionary theory with relevance to cancer and infections. The research is currently funded by 4 federal grants (NSF and NIH).
Mathematical models of carcinogenesis, cancer evolution, and therapy
A major component of our research program investigates cellular and evolutionary dynamics to understand how cancers initiate, progress, and evolve resistance, with the goal of improving therapies to prevent resistant tumor states. This work spans treatment-response dynamics, the evolution of drug resistance, the role of genetic instability, tissue stem-cell dynamics, escape from feedback control, the effect of feedback control on therapy outcomes, and tumor–microenvironment cross-talk. Some of these themes are discussed in our books Dynamics of Cancer: Mathematical Foundations of Oncology and Targeted Cancer Treatment in Silico. The following highlights selected examples from the past decade of this research.
Much of our work has focused on the hematopoietic system and hematopoietic malignancies. Recently, we discovered important principles that govern the emergence of mutant clones in hematopoietic stem cell lineages at homeostasis that can later lead to carcinogenesis. A new mathematical model, parameterized by hematopoietic stem cell label propagation data in mice, identified major barriers to mutant invasion, and predicted mechanisms based on aging and evolutionary niche construction that can eventually allow mutant growth (Komarova et al, 2024, PNAS). This can guide the development of conceptually new evolution-based therapies to reduce mutant burden. In modeling therapy responses and resistance evolution, we have used computational approaches to quantify and predict outcomes in chronic lymphocytic leukemia (CLL). Across several cohort studies (Wodarz et al., 2014, Blood; Burger et al., 2017, JCI Insight; Kim et al., 2024, Blood), we analyzed clinical data documenting CLL growth and responses to the BTK inhibitor ibrutinib, deriving patient-specific kinetic parameters. Contrary to prevailing assumptions, we showed that ibrutinib induces substantial CLL cell death within lymphoid tissues, with especially rapid death rates in patients carrying genetic markers historically associated with poor responses to chemotherapy. Using these parameter estimates, we developed the first evolution-based computational framework to predict resistance-driven relapse under ibrutinib therapy and to evaluate strategies for delaying resistance (Komarova et al., 2014, PNAS). We are now extending this framework to incorporate additional biological complexity.
We also worked on the evolutionary dynamics of solid tumors, in particular colorectal cancer. We developed an integrated experimental–theoretical approach to understand how aspirin alters tumor cell kinetics and how these effects scale to cancer prevention. First, in vitro and mouse xenograft studies were combined with computational modeling to quantify how pharmacologically relevant aspirin concentrations slow colorectal cancer cell proliferation and increase apoptosis across diverse mutational backgrounds (Zumwalt et al 2017, Cancer Prevention Research, Shimura et al 2019, Carcingogenesis). These data were used to build a multiscale computational modeling approach to bridge between an in vivo model of colorectal carcinogenesis and the epidemiologically observed age-incidence patterns of adenomas in patient cohorts that did or did not receive aspirin treatment for chemoprevention. A central result of this work was the discovery that the experimentally measured aspirin-induced fitness reductions of cells were sufficient to account for the magnitude of the epidemiologically observed protective effect of aspirin, through changing the evolutionary trajectories of cells (Wang et al 2022, eLife).






Dynamics of viruses and immune responses
We have a long-standing interest in virus–immune system dynamics, particularly the interaction between viral infections and cytotoxic T lymphocyte (CTL) responses, an important branch of the adaptive immune system to fight viral infections. Our work spans CTL memory, viral dynamics in murine systems, viral replication in CD4-deficient hosts, and HIV–immune interactions, with mathematical models applied to experimental data as a unifying theme. Some of these efforts are summarized in my book Killer Cell Dynamics.
In HIV research, we recently contributed to advancing “kick and kill” approaches aimed at depleting the latent reservoir during antiretroviral therapy (ART). Through interdisciplinary collaborations (Kim et al., 2022, Nature Communications; Zhang et al., 2025, Nature Communications), we combined mathematical modeling with genetically barcoded viruses to show that supplementing traditional kick-and-kill strategies with natural killer (NK) cells markedly reduced rebounding viral clones and diversity, identifying a new avenue for therapy optimization. Another project examined how the multiple infection of cells through direct cell-to-cell HIV transmission influences viral evolution. Modeling experimental data from humanized mice (Law et al., 2016, Cell Reports), we demonstrated that repeated co-transmission of genetically distinct variants creates intracellular interactions that can substantially alter evolutionary trajectories (Kreger et al., 2021, Virus Evolution).
Most HIV models assume a single well-mixed compartment, yet HIV replicates within lymph nodes divided into extrafollicular and follicular regions with markedly different CTL accessibility. Our recent work shows that this spatial structure has profound evolutionary consequences (Chung et al., 2024, Virus Evolution; Chung & Wodarz, 2025, J. Roy. Soc. Interface). Using computational models and SIV-infected macaque data, we found that strong CTL pressure in extrafollicular zones combined with weak pressure in follicles creates heterogeneous selection that slows CTL escape. Beyond escape, we showed that compartmental structure suppresses HIV evolution more broadly by lowering the fixation probability of mutants, reducing the mutant generation rate, and delaying the invasion of advantageous mutants, especially under strong CTL responses. Thus, lymphoid tissue architecture is a key determinant of HIV evolutionary dynamics and must be included in predictive models.
We also investigated oncolytic virus therapy. Our group helped pioneer computational modeling in this field, now widely used to guide therapeutic design. Recent work examined virus spread through spatially structured target cell populations characteristic of solid tumors (Rodriguez-Brenes et al., 2017, PLOS Comp. Biol.). Experiments tracking fluorescent adenovirus spread in 2D monolayers revealed two consistent outcomes under identical conditions: robust expanding plaques or stalled, limited infections. Computational modeling suggested that these divergent trajectories arise from interactions between viral spread and an innate immunity–induced antiviral state, a prediction confirmed by interferon inhibition experiments. These results highlight the complexity of early infection dynamics required for successful oncolytic virus propagation.

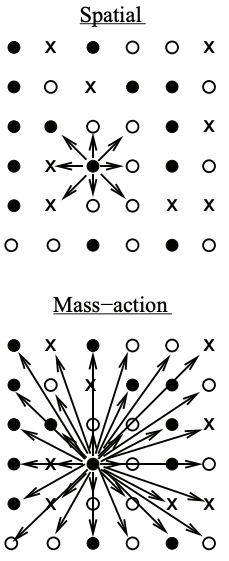
Evolutionary theory related to diseases
Evolutionary processes are central to our biomedical research, and we therefore develop new evolutionary theory, with a particular focus on spatially structured populations. We recently showed that predictions of mutant burden in expanding cell populations change fundamentally when spatial or patch structure is considered, deviating strongly from classical well-mixed theory (Wodarz & Komarova 2020, Genetics; Wodarz & Komarova 2023, Nature Communications). Building on this, we derived growth laws for single-hit, double-hit, and multi-hit mutants in spatially expanding populations across different dimensions (Komarova et al., 2025, PNAS Nexus). These scaling laws demonstrate that spatial structure allows intermediate cell states with elevated mutation rates (e.g., gene amplification or mismatch-repair deficiency) to contribute substantially to the emergence of target mutants, an effect largely absent in well-mixed systems. Another line of work examined mutants with simultaneously increased (or decreased) birth and death rates (“higher / lower turnover”), a common feature in tumors. Our computational models show that changed turnover can reverse selection in spatially structured populations (Komarova & Wodarz, Nature Communications, to appear): mutants with higher reproductive output may become strongly disadvantageous if turnover is increased, whereas mutants with lower reproductive output may become advantageous if turnover is reduced. This is the consequence of both spatial and stochastic mutant dynamics. These findings revise our understanding of how lifetime reproductive success correlates with selection, and reshape how we think about mutant emergence during cancer progression and therapy.

